經過了昨天的圓周運動，相信大家頭應該都有點暈吧，我自己是暈爆，今天應該會輕鬆一點！吧？

一樣唸一遍進入正題吧！

寐偲，天卷！！

數學課

sin跟cos講完了！當然不能夠漏掉tan～
一樣我們先來看看定義吧：
tan代表著一個角度的「正切值」，對於一個直角三角形的角來說就是對邊 / 鄰邊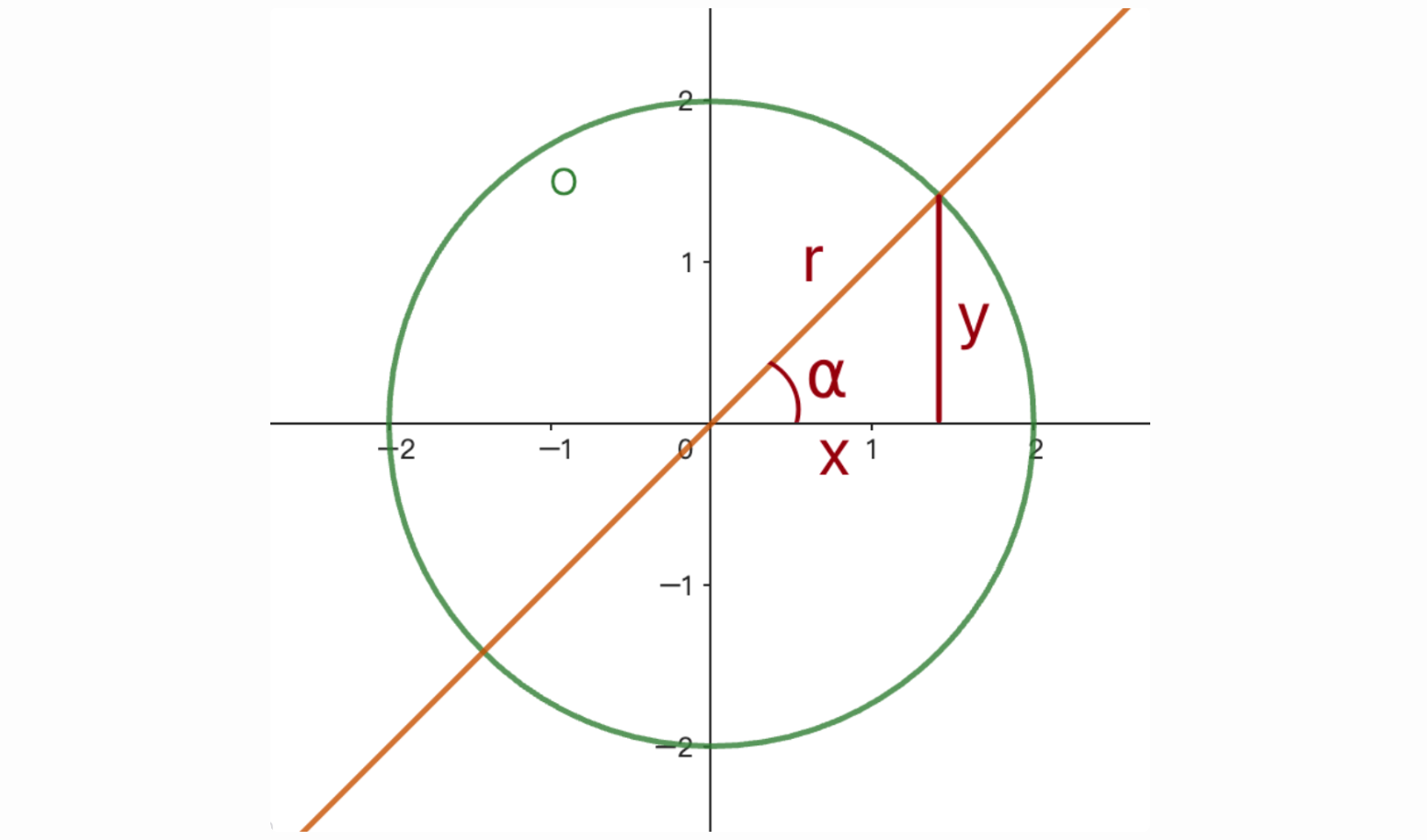

又是這個熟悉的圖呢！所以正切值tanα就會是y / x！

正切值tan也有幾個好觀察的值：
tan0° = 0
tan45° = 1
tan135° = -1
tan180° = 0

不免俗的來看一下y = tanx的圖形吧：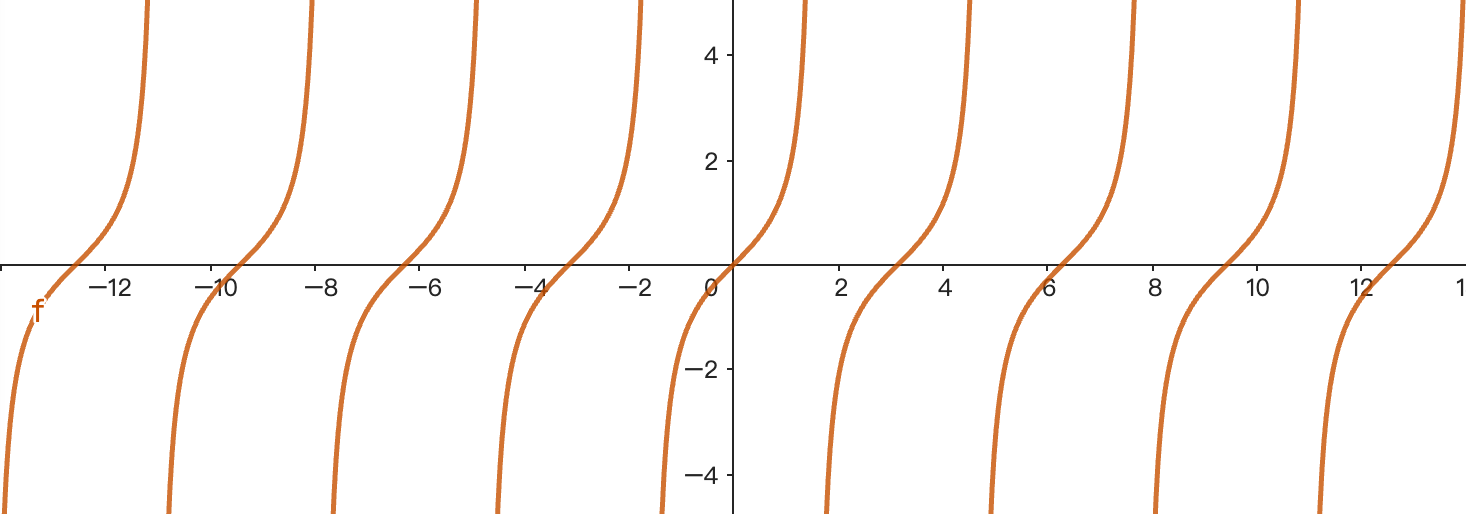

觀察到tanx的值會在x = 0或是x = π的時候為0，隨著x的增加，tanx也慢慢往上爬到無限大，直到x = π / 2的時候跳到負無限大，再慢慢往上爬到無限大，不斷重複這個循環，每增加π就為一個循環，但看完這個特性我也想不出來可以幹嘛。

OKOK，我相信大家覺得差不多了，再來看看到底如何使用吧！

Math.tan()

語法

Math.tan(x)

參數

傳入一個以弧度表示的數值

回傳值

回傳x的正切值，如果x是Infinity、-Infinity或NaN，回傳NaN。

規範

這個函式會回傳x的正切值。

除了一些針對tan的細節，其他都跟前面講的sin跟cos大致一樣了哇哈哈！

測試看看剛剛提到好觀察的點吧！

Math.tan(0); //0
Math.tan(Math.PI / 4); //0.9999999999999999
Math.tan(Math.PI * 3 / 4); //-1.0000000000000002
Math.tan(Math.PI); //-1.2246467991473532e-16 

又是熟悉的誤差呢哈哈，所以使用上一定要注意！

應用

可以幹嘛呢～～

到處看來看去，想出了一個不知道有沒有用的應用哈哈哈！
我們來模擬一個遊戲視角的範圍計算吧！
先來看看大致上想算什麼東西吧：

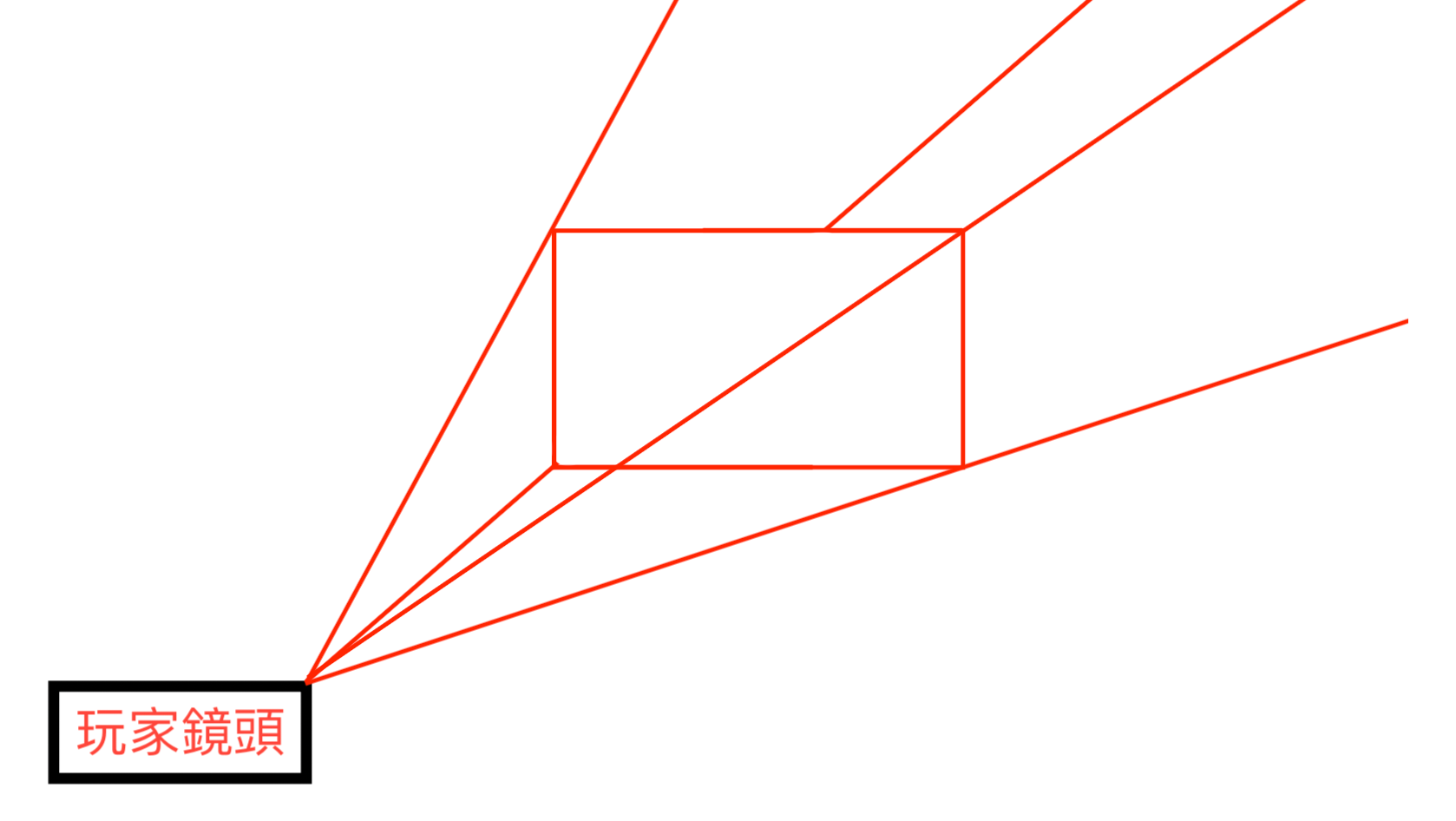
先想像一個遊戲情境，螢幕是長方形的，玩家透過鏡頭看出去某個距離的截面就是紅色框框，我們需要知道紅色框框的上下左右邊界就能決定在距離玩家多遠的截面實際要顯示多少內容。

從側面看：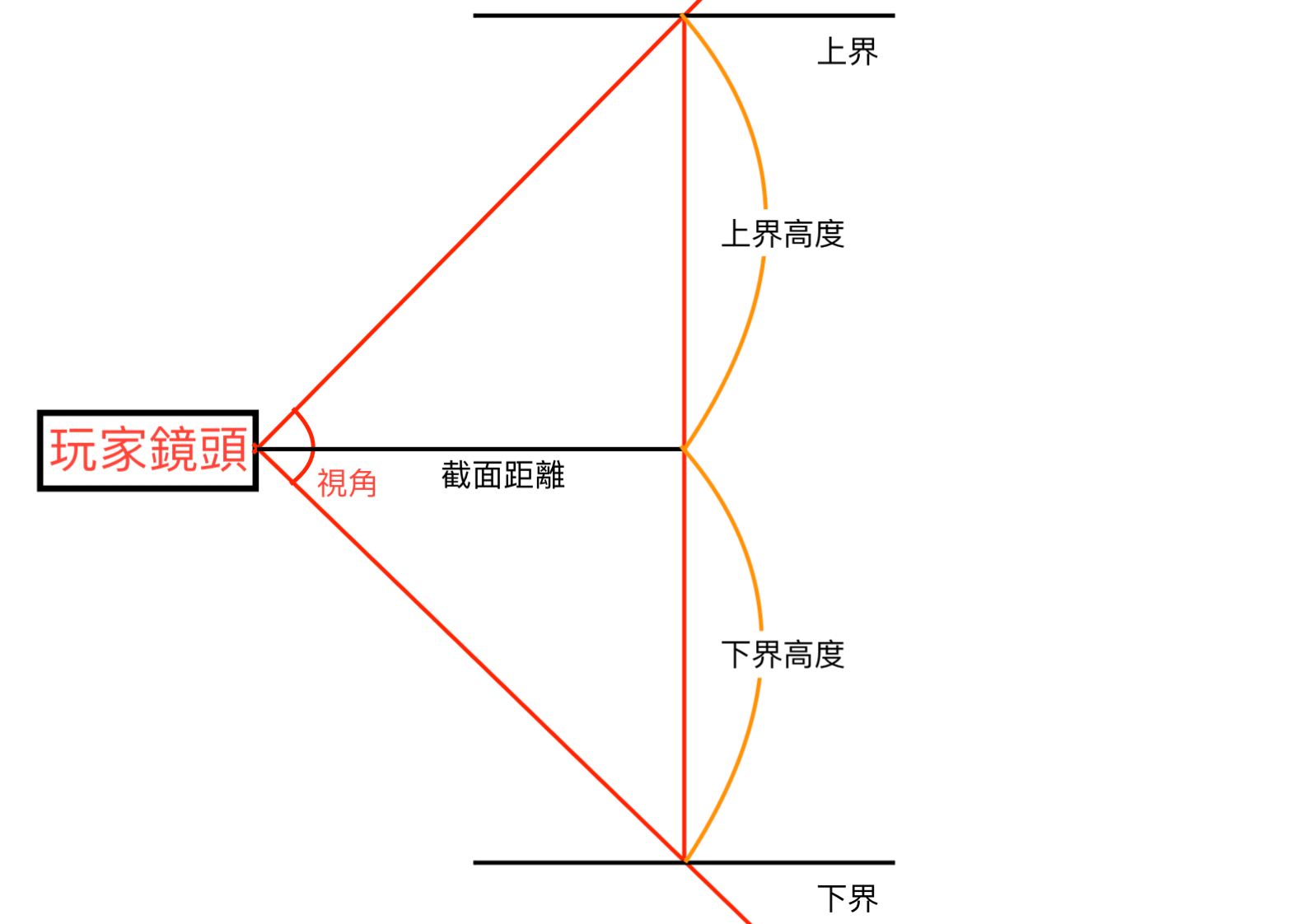

假設玩家鏡頭高度位置定為0，那我們算出上界位置，下界就是上界的相反數，這樣我們就可以知道在距離玩家某個距離的截面上下要顯示的內容到哪，在範圍內的才渲染出來，範圍外的就不渲染，左右邊界也依此類推。

那就來嘗試算算看吧！

const angleOfView = 90; //視角
const aspectRatio = 16 / 9; //螢幕長寬比
const distance = 0.1; //與鏡頭的距離

const angleOfViewInRadians = (angleOfView * Math.PI) / 180; //將視角轉換成弧度等等要給tan

const position = {};

position.top = distance * Math.tan(angleOfViewInRadians / 2);
position.bottom = -position.top;
position.right = position.top * aspectRatio;
position.left = -position.right;

console.log(position);

雖然有誤差，但在座標平面上視覺是幾乎看不出差別的。

這樣我們就能透過視角與螢幕長寬比來得到不同距離的截面邊界了！

知道距離跟視角

寐偲，天卷！！！

直接找出邊界高度。

明天要學什麼咒語呢～～

參考資料：
MDN-Math.tan()
ECMAScript-Math.tan()